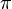 (pí), a Ludolph-féle szám
(pí), a Ludolph-féle szám
- A
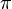 (pí) a görög abc egyik betűje-szimbólum a kör kerületének és az átmérőjének az arányát jelenti, azaz
(pí) a görög abc egyik betűje-szimbólum a kör kerületének és az átmérőjének az arányát jelenti, azaz 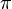 =k/d, amely bármely kör esetén egy állandó szám. Bár a p két szám hányadosa, mégsem racionális szám., azaz vagy a kör kerülete, vagy az átmérője vagy mindkettő irracionális szám. Magát a számra vonatkozó
=k/d, amely bármely kör esetén egy állandó szám. Bár a p két szám hányadosa, mégsem racionális szám., azaz vagy a kör kerülete, vagy az átmérője vagy mindkettő irracionális szám. Magát a számra vonatkozó 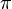 (pí) szimbólumot Euler javasolta 1739-ben.
(pí) szimbólumot Euler javasolta 1739-ben. - p rövid, vázlatos története.
- Már a Bibliában, az Ószövetségen is találkozhatunk vele. A királyok könyve 7.23.-ban ezt olvashatjuk: „… Aztán öntött egy medencét is. 10 könyököt tett ki egyik peremétől a másikig, magassága 5 könyök, és egy 30 könyöknyi zsinór érte körül.” Itt tehát az átmérő 10 egység, a kerület 30 egység, így
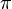 (pí) -re 3-t kapunk.
(pí) -re 3-t kapunk. - Az ókori egyiptomiak a kör területét a t = (d-d/9)2 képlettel számolták, ahol d a kör átmérőjét jelöli. Ők tehát a
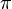 (pí) helyett a 256/81 = 3,1605 számmal dolgoztak.
(pí) helyett a 256/81 = 3,1605 számmal dolgoztak. - Arkhimédész a
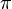 (pí) értékét a körbe írt 96 oldalú szabályos sokszög területével közelítette meg. Ő a azaz egyenlőtlenséget adta meg. Ez két tizedes pontosság.
(pí) értékét a körbe írt 96 oldalú szabályos sokszög területével közelítette meg. Ő a azaz egyenlőtlenséget adta meg. Ez két tizedes pontosság. - Apollóniosznak állítólag sikerült megállapítania a
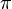 (pí) első négy tizedesét, de erről biztosat nem lehet tudni, mivel Apollóniosznak sok műve elveszett.
(pí) első négy tizedesét, de erről biztosat nem lehet tudni, mivel Apollóniosznak sok műve elveszett. - Ptolemaiosz „Almagest” című művében a
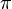 (pí) meghatározására a törtet használta, amely már 3 tizedesre pontos érték.
(pí) meghatározására a törtet használta, amely már 3 tizedesre pontos érték. - A középkorban Viete francia matematikus végtelen sorozat segítségével a
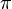 (pí) értékét 10 tizedesig számolta ki.
(pí) értékét 10 tizedesig számolta ki. - Ludolph Van Ceulen az 1600-as évek elején már 35 tizedesjegyig kiszámította az értékét.
p»3.141592653589793238462643383279502884197169399
Ezért szokás a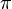 (pí)-t Ludolph-féle számnak nevezni.
(pí)-t Ludolph-féle számnak nevezni. - Ma már a számítógépek korában a
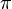 (pí) értékét több mint 16 millió tizedesjegyig kiszámították. Ha kiváncsi a
(pí) értékét több mint 16 millió tizedesjegyig kiszámították. Ha kiváncsi a 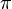 (pí) első 2000 számjegyére, kattints ide.
(pí) első 2000 számjegyére, kattints ide. - Csak a XVIII. században tudták kimutatni, hogy a
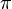 (pí) irracionális szám.
(pí) irracionális szám. - 1882-ben Lindemann német matematikus azt is kimutatta, hogy
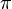 (pí) nemcsak irracionális, hanem transzcendens is, azaz nem lehet gyöke semmilyen racionális együtthatójú algebrai egyenletnek. Ez azt is jelenti, hogy a
(pí) nemcsak irracionális, hanem transzcendens is, azaz nem lehet gyöke semmilyen racionális együtthatójú algebrai egyenletnek. Ez azt is jelenti, hogy a 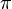 (pí) euklideszi szerkesztéssel nem szerkeszthető meg, de több jó közelítő szerkesztési eljárás is született az idők során. Az egyik legismertebbet itt megtalálod.
(pí) euklideszi szerkesztéssel nem szerkeszthető meg, de több jó közelítő szerkesztési eljárás is született az idők során. Az egyik legismertebbet itt megtalálod.
- Már a Bibliában, az Ószövetségen is találkozhatunk vele. A királyok könyve 7.23.-ban ezt olvashatjuk: „… Aztán öntött egy medencét is. 10 könyököt tett ki egyik peremétől a másikig, magassága 5 könyök, és egy 30 könyöknyi zsinór érte körül.” Itt tehát az átmérő 10 egység, a kerület 30 egység, így
- A pí kiszámítása, közelítések.
- Az alábbi sort Leibnizről nevezték el, de nem ő fedezte fel, hanem valószínűleg James Gregory szkót mathematikus:
- 1669-ben John Wallis szintén skót mathematikus (1616. 12. 03 – 1703. 11. 08.) sora:
- 1706-ban Machin francia mathematikus
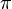 (pí)-hez gyorsan közeledő sora:
(pí)-hez gyorsan közeledő sora: - Euler a következő sorral számolt:
Itt mindkét zárójelben a tagok nagyon gyorsan csökennek, így már 7-7 tag esetén igen pontos eredményt kapunk.
- Matematikai és kultúrtörténeti érdekességek az un.
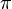 (pí) versek.
(pí) versek.
Ha érdekli, kattintson ide!
Forrás : http://www.bethlen.hu
Ha tetszik írásunk, ajánlhatja másoknak is!
A túlélés útja ma magyarul gondolkodni...














 Európa szívéből
Európa szívéből